Emergence Theory and the Golden Ratio
Emergence theory predicts a fundamental, natural phenomenon that is so strange yet so prevalent that, with no physics theory having ever explained it, has been largely ignored by the scientific establishment and often seen as the stuff of amateur scientists and hobbyists. This phenomenon is the ubiquity of the golden ratio in nature from the micro (including the Planck scale) to the macro scale. Upon learning of a golden ratio related fact, most scientists will often treat it as a coincidence. However, the statistical probability of the golden ratio’s unrelenting prevalence to such high accuracy is practically zero.
The “golden ratio” (sometimes called the “golden mean” or “golden section”) is a fundamental geometric ratio that appears in a circumscribed equilateral triangle.
The value of the golden ratio is 0.618 or 1.618. It is an irrational number often symbolized by the Greek letter “phi” ( Φ, φ ) and can be expressed by this formula:
![]()
Many of the ways the golden ratio (as well as its rational form, the Fibonacci sequence) appears in nature are well-known – a quick list of examples includes flower petals, seed heads, pine cones, shells, spiral galaxies, hurricanes, faces, DNA molecules and many more. None of this is new. It would be news to many people, however, that the golden ratio makes many precise (100% accuracy) and near-precise (accuracy of and near 99.99…%) appearances in values related to astronomical bodies that are often surprising and interesting. For example it appears, notably, in black hole physics: the golden ratio is precisely the point where a black hole’s modified heat changes from positive to negative, and it is part of the equation for the lower bound on black hole entropy. The golden ratio even relates to the loop quantum gravity parameter to black hole entropy. The three formulas respectively can be seen in this graphic:
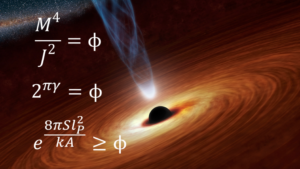
Therefore, the golden ratio may be the fundamental constant of nature.
Black holes are where general relativity and quantum mechanics converge at their limits. Any unification model (“theory of everything”) must include these two theories. In binary matrices, which were used by Heisenberg to describe quantum mechanics, the highest probability non-trivial eigenvalues are the golden ratio, and negative one over the golden ratio. The golden ratio appears fundamentally in quantum mechanics and in black holes. The golden ratio appears in atoms as well. The atomic radius of hydrogen in methane is the Bohr radius over the golden ratio. In 1993 Lucien Hardy of the Perimeter Institute discovered that the probability of entanglement for two particles projected in tandem is the golden ratio over negative 5.
Emergence theory is based deeply on the notion of language. A powerful language is one which has the ability to express the maximum amount of meaning with the least number of choices, since each choice requires resources. A resource in this sense can be a unit of electricity spent for a logic gate to be opened to activate a binary choice in a computer language, or a calorie or two of energy needed to make a mental choice of what shirt to wear. For those philosophically inclined, even a universe made of consciousness might be interested in conserving that precious resource to express the most physical meaning. Most can agree that the most foundational principle of physical reality is the principle of least action. Clearly, the universe is in the business of expressing physical meaning. And, for some reason, it does this in the most economical way possible, as though it’s interested in getting the biggest “bang for the buck” of whatever the foundational stuff of reality is. Materialists say that stuff is “energy”, but they are not able to explain or define exactly how energy is anything other than abstract information. And a growing number of physicists, from the late John Wheeler to MIT’s Max Tegmark, tell us that it is trivially obvious from the implications of both classic and quantum physics that reality is indeed made of information. Now, that’s interesting. Because information is meaning conveyed by symbolism. Typical meaning, such as humor, is very subjective, while mathematical and geometric meaning is less subjective. For example, if a square were a symbol that represented the object known as a square, with its 90 degree angles and other intrinsic not-so-subjective attributes, it would be an excellent candidate for the type of symbolic language that an information-only reality might be made of.
After all, physical reality is geometric.
And this is where the golden ratio comes in. Quasicrystals are golden ratio based geometric languages. They are codes made of geometric symbols. Since reality is three dimensional, we suggest to look first to see if reality might be written in the code 3D quasicrystals. Time and motion could simply be ordered sequences of different 3D quasicrystal configurations, “played” rapidly like a 3D strip of film frames. Ideas like the invariance of the speed of light could be explained using new ideas like an update of the de Broglie electron clock model.
Any 3D quasicrystal is really just an interactive network of 1D quasicrystals. The most foundational and simplest 1D quasicrystal, the Fibonacci chain, has two geometric “letters” in its language. (Yes, quasicrystals are languages or codes because they fully meet the definition by having (1) a finite set of two or more symbols, (2) symbol matching rules and (3) syntactical degrees of freedom.) The two geometric letters in a Fibonacci chain quasicrystal are lengths with a ratio of one to the other that is the golden ratio, where the long length has a ratio to the short length that is the same ratio as the long length to the sum of the long + short length. It’s the only ratio in math that switch hits like this.
Languages that have a lot of letters are costly. Imagine if the English language had 23 million letters! Working with it would be mentally difficult and would certainly not conserve choices. Let’s clarify: all choices are not equally resource intensive. Does it require more mental energy to choose between vanilla and chocolate or to choose from 100 delicious flavors of ice cream? Similarly, languages with fewer letters require less resources for each choice of letter. This is one reason why this text you’re reading is expressed as binary code under the secondary level of English words. In a geometric code, like the quasicrystal code nature might be using, a two letter code might be powerful as well. And the only way to get networks of 1D codes to act as an interactive 3D network of 1D codes is to use the golden ratio. Explaining that might take a bit more time and a little math. But suffice it to say that the golden ratio is a powerful tool for building physics.

