The QSN and Its Mapping to E8
The Quasicrystalline Spin Network (QSN) is a 3D quasicrystalline point space on which we model physics. The QSN is deeply related to the E8 crystal. The following is a brief explanation of the relationship between the various related objects.

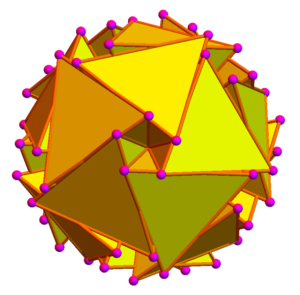
We begin with an 8-dimensional crystal called the E8 lattice. The E8 lattice is an 8D point set representing the densest packing of spheres in 8D. The basic cell of the E8 lattice, the Gosset polytope, has 240 vertices and accurately corresponds to all particles and forces in our (3D) reality and their interactions, specifically the way they can all transform from one to another through a process called gauge symmetry transformation (you can view a Ted Talk by Garret Lisi on this subject here).
The first operation we perform is to take the E8 lattice and project a slice of it to 4D, through one of two processes: cut-and-project, or Hopf mapping. Either process gives us the same result: a 4-dimensional quasicrystal called the Elser-Sloane quasicrystal. When the E8’s basic cell, the Gosset polytope, is projected to 4D, it creates two identical, 4D shapes of different sizes. The ratio of their sizes is the golden ratio. Each of these shapes is constructed of 600 3-dimensional tetrahedra rotated from one another by a golden ratio based angle. We refer to this 4D shape as the “600-Cell.” The 600-Cells interact in specific ways (they intersect in 7 golden ratio related ways and “kiss” in one particular way) to form the 4D quasicrystal. This is a representation of the two 600-Cells that make up the 4D quasicrystal.
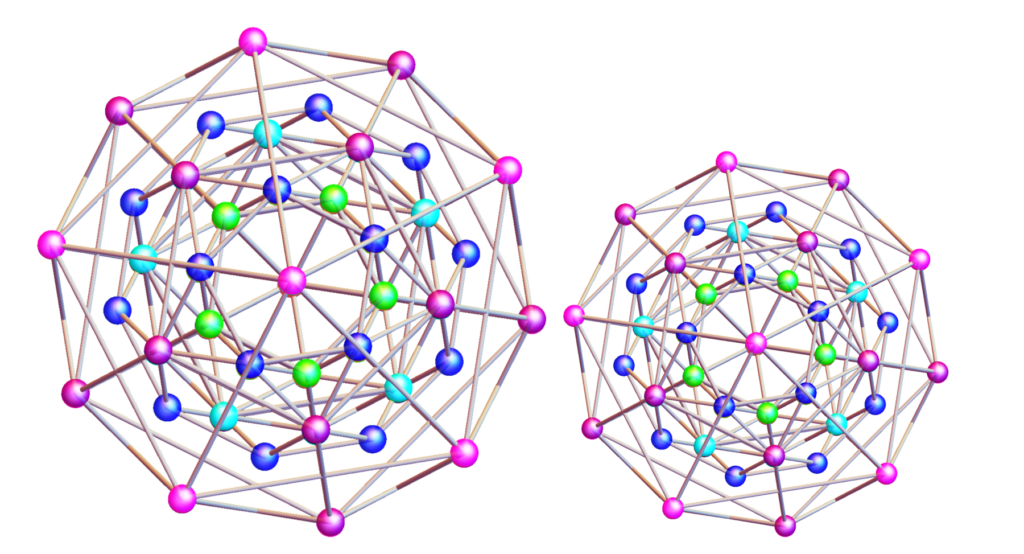
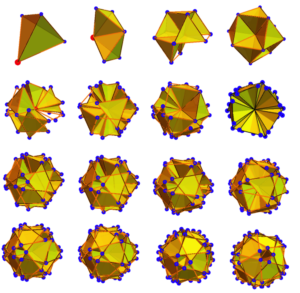
Next we take five 3D subspaces, or tetragrid, of this 4D quasicrystal (one subspace being all tetrahedra that are oriented in the same direction) and then rotate them from one another by 15.522 degrees, we come up with a 3D quasicrystal that can be seen as a representation of the 4D, Elser-Sloane quasicrystal. We call this the “Compound Quasicrystal” (CQC). Here is a representation of five subspaces – the image on the left is one subspace, the second one has a second subspace layered onto it and so on. The fifth image is the CQC.

Why is the Compound Quasicrystal important? It is important because of its relationship to the QSN. The QSN (Quasicrystalline Spin Network) is the densest possible (under certain constraints) 3D network of point-sharing Fibonacci chains and is the most computationally efficient point space in 3D. When we talk about the densest 3D Fibonacci chain, we are talking about two letter chains instead of the infinitely inflated chains, which is a property of QSN as a quasicrystal. The QSN is created by taking the FCC lattice (a point space that provides the densest packing of 3D spheres) and then spreading its points until they are spaced according to the Fibonacci sequence. We populate this new, extended point space with tetrahedra that point up and that point down. Here is a close up of what that looks like:

Let’s call the tetrahedra pointing up “subspace 1” and the tetrahedra pointing down “subspace 2.” We take new lattice of Fibonacci spaced points, clone it five times and as we did with the subspaces that formed the Compound Quasicrystal, rotate the five clones from one another by 15.522 degrees to create a new quasicrystal. We then repeat the process with subspace 2. Subspaces 1 and 2 are combined to create the QSN. In this sequence of images we see 5 clones of 4 tetrahedra in one subspace – each clone in a different color – being rotated from one another. The 4 tetrahedra share a vertex, and the object that is created from the 5 rotations of them is called a 20-Group.

The QSN is composed of tetrahedra that form many different vertex types. The above mentioned 20-Group is one of them. Here are examples of other vertex types:
This is the QSN:

And now to the connection between the QSN, which started its life as the point space representing the most efficient sphere packing in 3D, and the 4D-quasicrystal-derived Compound Quasicrystal, which started its life as E8, the most efficient sphere packing in 8D: as it turns out, the Compound Quasicrystal is an exact subspace of the QSN. The QSN contains all legal configurations of the Elser-Sloane, 8D-to-4D quasicrystal.
The QSN is therefore deeply related to the E8 lattice and its 4D projection.
In simplistic terms, you can think of the QSN as a 3D version of a 2D TV screen. A 2D TV screen is made up of 2D pixels that change brightness and color levels from one video frame to the next at a certain speed (for example 24 frames per second in most modern movies).
Now we can use our QSN geometry as a toy model for physics!
Similarly, the QSN is a 3D grid of Planck scale, tetrahedron-shaped “pixels” that, via the rules of a binary, geometric language/code, exist at each “frame” of reality as either on or off, and if on, then rotated left or right. These pixels populate the QSN, and their states change from one frame to the next, at a “universal frame rate” of 10^44 frames per second (the “Planck time”) Over many of these frames patterns emerge on this 3D quasicrystal. These patterns become more and more meaningful and sophisticated with time. After a while, particles begin to form on the quasicrystal. With time, these particles take on more and more complex forms, and eventually the reality we all know, love and play video games in, emerges.

